Basics of 2D Coordinate Geometry

In what ratio does the point $(-4, 6)$ divides the line segment joining the points $A(-6, 10)$and $B(3, -8)$?

The distance between points $(2, 5)$and $(7, -3)$ is

From the point $A\left(0,3\right)$ on the circle $x^2+4x+{\left(y-3\right)}^2=0$, a chord $AB$ is drawn and extended to a point $M$ such that $AM=2AB$. The equation of the locus of $M$ is

If the area of a triangle is $4$ sq. units with vertices at $\left(–2, 0\right),\left(0, 4\right)$ and $\left(0, k\right)$, then the value of $k$ is

If $x_1,x_2,x_3$ and $y_1,y_2,y_3$ are both in G.P. with the same common ratio, then the points $\left(x_1,y_1\right),\left(x_2,y_2\right)$ and $\left(x_3,y_3\right)$

Consider a rigid square $ABCD$ as in the figure with $A$ and $B$ on the $X$ and $Y$-axes, respectively.

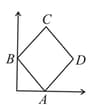
When $A$ and $B$ slide along their respective axes, the locus of $C$ forms a part of

What is the distance of point $\left(5, 12\right)$ from the origin?

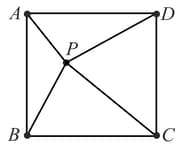
Square $ABCD$ has side length $30.$ Point $P$ lies inside the square so that $AP=12$ and $BP=26.$ The centroids of $∆ABP, ∆BCP, \Delta CDP$ and $∆DAP$ are the vertices of a convex quadrilateral. The area (in sq. units) of the quadrilateral is

Define $2\mathrm{D}$ coordinate system. Find the quadrant $(4,-2)$ belongs to.

Define $2\mathrm{D}$ coordinate system. Find the quadrant $(1,-2)$ belongs to.

Define $2\mathrm{D}$ coordinate system. Find the quadrant $(-1,-2)$ belongs to.

Define $2\mathrm{D}$ coordinate system. Find the quadrant $(-1,2)$ belongs to.

Define $2\mathrm{D}$ coordinate system. Find the quadrant $(1,2)$ belongs to.

If a square $ABCD$ where $A(0,0),B(2,0),C(2,2),D(0,2)$ undergoes the following transformations successively,

$\left(\mathrm{i}\right)$ $f_1(x,y)⟶(y,x)$
$\left(\mathrm{ii}\right)$ $f_2(x,y)⟶(x+3y,y);$

$\left(\mathrm{iii}\right)$ $f_3(x,y)⟶\left(\frac{x-y}{2},\frac{x+y}{2}\right)$

Then the final figure would be a _______.

Given points $A(6, 0), B(0, 4)$ and $O$ as the origin, find the locus of a point $P$ such that area of triangle $POB$ is $2$ times the area of triangle $POA.$

For two points $A(2, 1)$ and $B(1, 2), \text{'}P \text{'}$ is a point such that $PA: P B=2:1,$ then locus of $P$ is

If the equation of a line which divides the line segment joining the points $\left(1,0\right)$ and $\left(3,0\right)$ in the ratio $2:1$ and is also perpendicular to it, is $ax=7$, then the value of $a$ is equal to

Let $P_1, P_2$ be any two points on a circle of radius $r$ centred at the origin $O,$ such that $\angle P_{1}O{P}_2=\frac{\pi }{3},$ If $P$ is the point of intersection of the tangents to the circle at $P_1$ and $P_2,$ then the locus of the point $P,$ is

If the point $R$ divides the line segment joining the points $\left(2,3\right)$ and $\left(2\tan \theta ,3\sec \theta \right) ; 0<\theta <\frac{\pi }{2}$, externally in the ratio $2:3$, then the locus of $R$ is

Let $S$ be the focus of parabola $x^2+8y=0$ and $Q$ be any point on it. If $P$ divides the line segment $SQ$ in the ratio $1 : 2,$ then the locus of $P$ is